
[241/242]
171
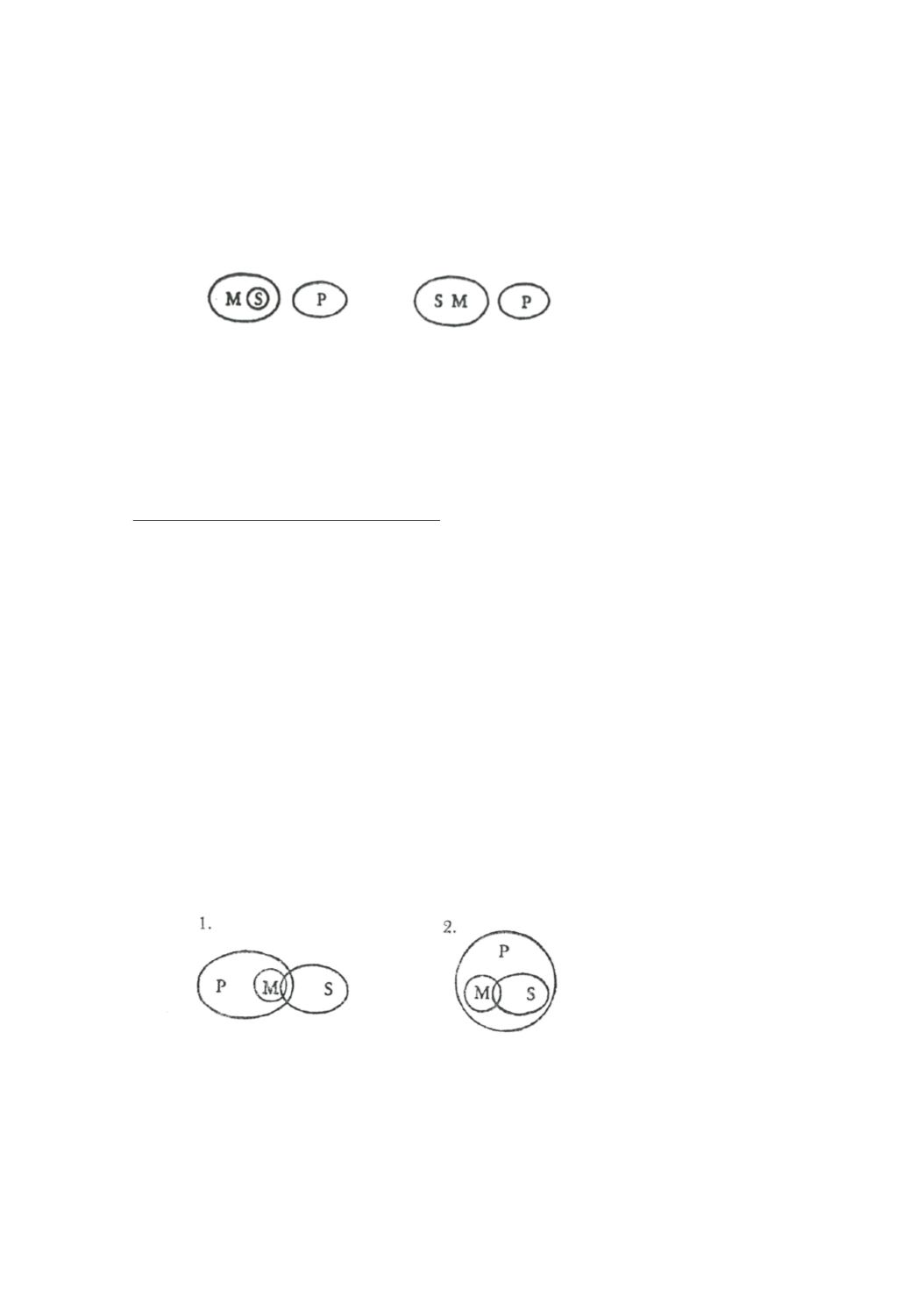
Die Sphärenbetrachtung ergibt das Bild:
1.
2.
In jedem Falle ist P von M getrennt, daher muß auch S, das ganz
in M liegt, von P getrennt sein. — Celarent ist dasselbe wie Bar-
bara, nur mit einem allgemein verneinenden Obersatze, daher auch
einem verneinenden Schlußsatze.
3.
Modus: D a r i i. Er hat die Form:
M a P Alle Quadrate sind geradlinige ebene Figuren.
S i M Einige Parallelogramme sind Quadrate.
S i P Also sind einige Parallelogramme geradlinige ebene Figuren
— in W a h r h e i t s i n d a b e r a l l e Q u a d r a t e P a r a l -
l e l o g r a m m e ! Es wird also in diesem und jedem Falle nach
Darii f a l s c h g e s c h l o s s e n . Überweg verteidigt diesen Mo-
dus wie folgt: „Der Wert dieses Schlußmodus, sowie aller anderen
in den verschiedenen Figuren, die mit ihm in gleichem Falle sind,
wird durch diese Unbestimmtheit zwar beschränkt, aber nicht auf-
gehoben. Denn es ist hier nicht alles unbestimmt, sondern nur das-
jenige, worüber aus den Prämissen nichts folgt. Es ist immer schon
ein Gewinn zu wissen, daß einigen S das P zukomme (oder in an-
deren Modi mit partikular verneinendem Schlußsatze, daß einigen
S das P nicht zukomme)“
1
.
/
Die Sphärenbetrachtung erweist sich in diesem Falle besonders
deutlich als ein bloß nachhinkendes, nicht beweisendes Bild:
1
Friedrich Überweg: System der Logik und Geschichte der logischen Lehren,
2. Aufl., Bonn 1865, S. 295 f.









