
[141/142]
103
dert, so die Weltwirtschaft mehrere Volkswirtschaftskreise, diese
mehrere Volkswirtschaften, oder der Staat mehrere Gaue, diese
mehrere Kreise, die höheren Säugetiere nebeneinander: Nagetiere,
Huftiere, Raubtiere und so fort auf gleicher Stufe. Das ergibt fol-
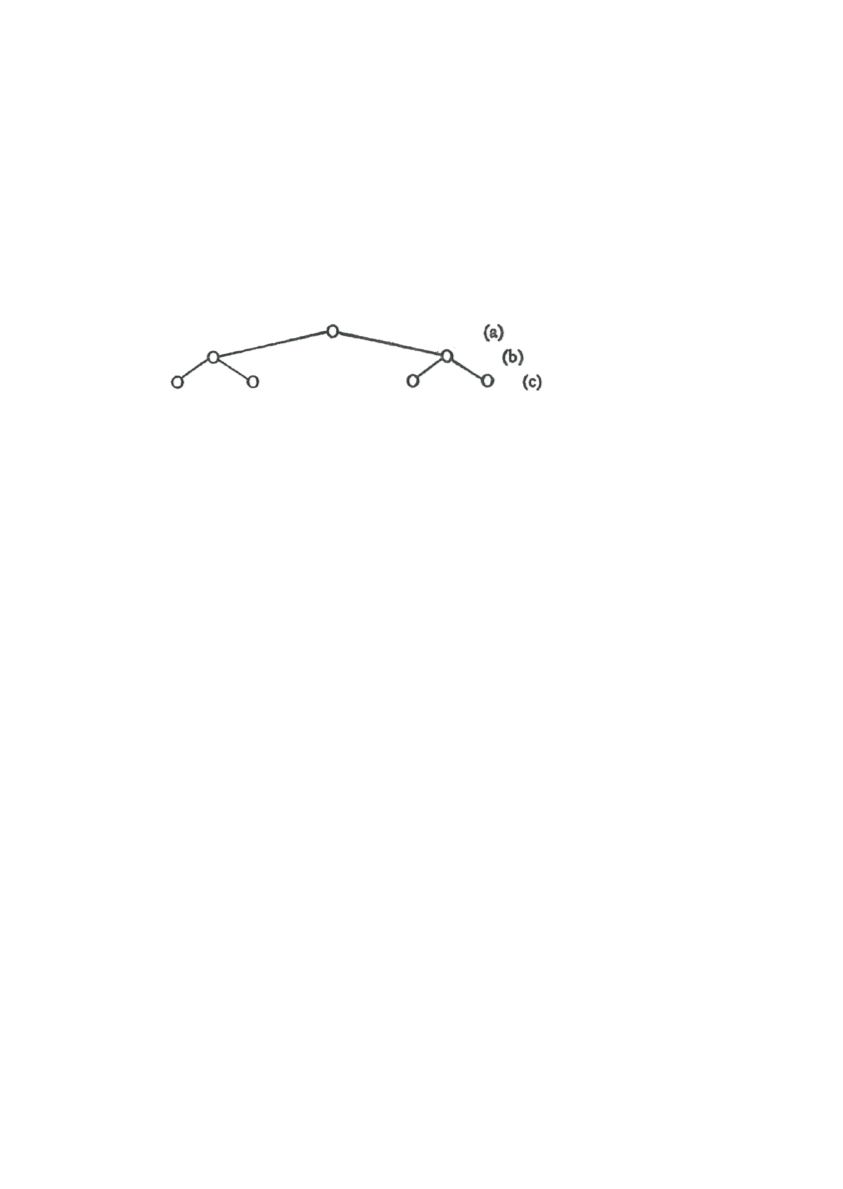
gendes Bild:
Die Begriffe „b“ und „c“ sind jeweils (unter sich) nebengeordnet.
In der ganzheitlichen Grundform „ N e b e n o r d n u n g “ liegt
ein nicht genug zu beachtender Grundbegriff (1) der logischen Ein-
teilungslehre, Urteilslehre, Schlußlehre und zugleich auch (2) eine
Ausschließung, ein Verneinendes.
Während nämlich im Stufenbau nach oben und unten, wie sich
zeigen wird, ein Einschließen und Eingeschlossenwerden stattfindet,
liegt in der Nebenordnung der Glieder eine A u s s c h l i e ß u n g !
In der Nebengeordnetheit eines Gliedes zum andern liegt nicht
Einerleiheit (diese liegt nur im Eingeschlossensein durch ein gemein-
sames Höheres), vielmehr Anderheit, weil Ausgeschlossensein vom
anderen; darin wieder: G e g e n s a t z , W i d e r s p r u c h und
weiterhin V e r n e i n u n g !
/
Wer diesen Ursprung des Begriffes des Gegensatzes bedenkt, ver-
steht, wie recht H e g e l hatte, als er mit Nachdruck behauptete,
daß der B e g r i f f e n t g e g e n g e s e t z t e B e s t i m m u n -
g e n i n s i c h s c h l i e ß e ! Denn die Nebenordnung beruht ja
darauf, daß eine Ganzheit m e h r e r e Glieder der nächsten Stufe
ausgliedere; „mehrere“ heißt aber, daß im Inneren des Ausglie-
dernden G e g e n s ä t z e bestehen.
Nun fragt es sich allerdings, welche? Die schlechthin ausschlie-
ßenden, in der formalen Logik k o n t r a d i k t o r i s c h e ge-
nannt
1
, können es nicht sein. Denn wenn ein und dieselbe Ganzheit
mehrere Glieder derselben Stufe ausgliedert, muß bei aller Ander-
heit, Unterschiedlichkeit, Gegensätzlichkeit auch ein G e m e i n -
s a m e s sein. Wir müssen daher die in der Nebenordnung liegenden
1
A-non-A, siehe oben S. 53 und 78.









